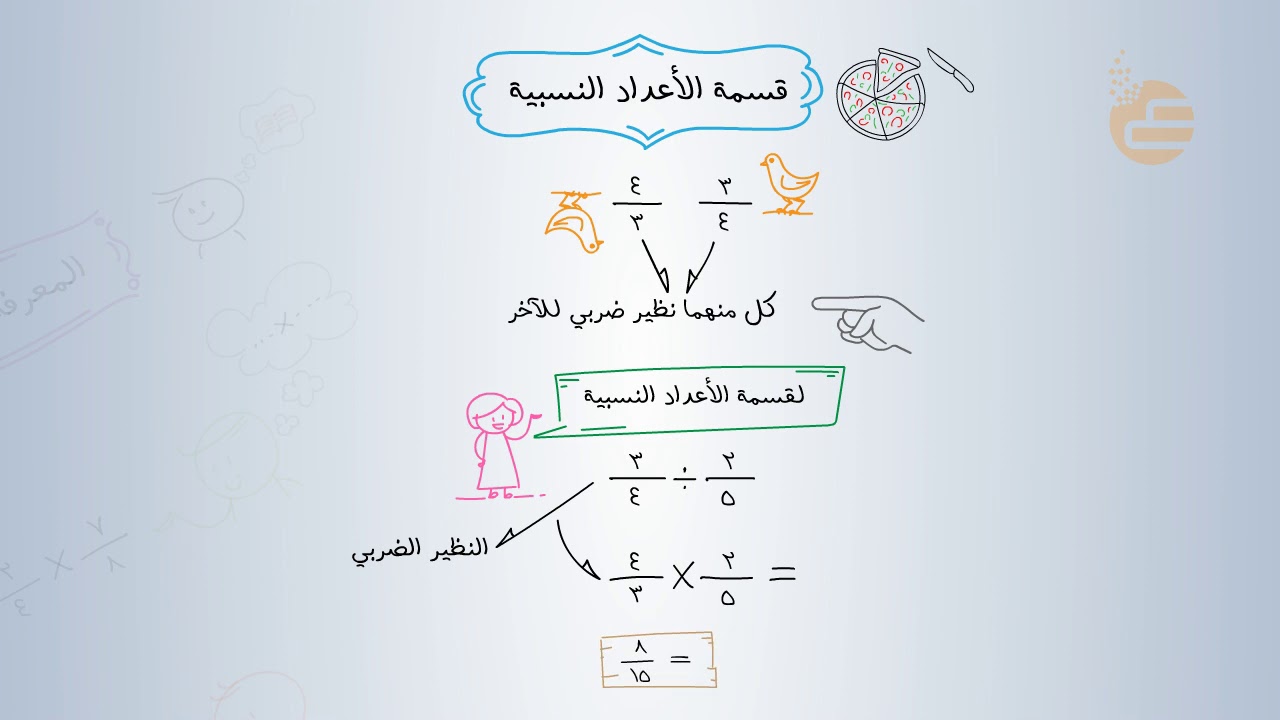
في عالم الرياضيات، تعد الأعداد النسبية مصطلحًا مهمًا. إنها وسيلة للتعبير عن العلاقات النسبية بين الكميات. في حين يتم تمثيل الأعداد المطلقة في شكل أرقام, فإن الأعداد النسبية تستخدم للتعبير عن قوة أحداث.
تعريف الأعداد النسبية وما يمثلها
الأعداد النسبية: هي أرقام تستخدم للتحكم في توزيعات الكميات المختلفة. على سبيل المثال، إذا كان هناك 5 فقراء و 10 أثرياء في مجتمع، يمكن استخدام الأعداد النسبية لوصف هذه المجتمعات وفحص التغيرات في التوزيع.
الأعداد المئوية: هي نوع آخر من الأعداد النسبية يستخدم لوصف التغيرات في التوزيع. تُعبر الأعداد المئوية بنسبة المئوية من قوة حدث ما بالنسبة للمجتمع بأكمله.
مفهوم الأعداد النسبية مهم في الاقتصاد، حيث يستخدم لتحليل البيانات وفهم التغيرات في التوزيع. قد يساعد فهم هذه الأعداد في اتخاذ قرارات أفضل وتحديد الاحتياجات والمشكلات في المجتمع والإشارة إلى الفجوات.
كيفية تحويل الأعداد إلى نسب
عندما يتعلق الأمر بالأعداد النسبية، يعتبر تحويل الأعداد العادية إلى أعداد نسبية خطوة مهمة. الأعداد النسبية هي عبارة عن قياسات تستخدم للتعبير عن العلاقة بين جزء وكل في مجموعة. تحويل الأعداد إلى أعداد نسبية يساعد في فهم وتحليل البيانات بشكل أفضل.
طرق تحويل الأعداد إلى أعداد نسبية
- النسب المئوية: تستخدم النسب المئوية للتعبير عن حجم جزء ما من الكل. لحساب النسب المئوية، يجب ضرب قيمة الجزء في 100 ثم قسمتها على قيمة الكل.
- النسب المئوية المئوية: تستخدم النسب المئوية المئوية للتعبير عن حجم جزء من جزء ما من الكل. لحساب النسب المئوية المئوية، يجب ضرب قيمة الجزء الصغير في 100 ثم قسمتها على قيمة الجزء الكبير.
- النسب المئوية التراكمية: تستخدم النسب المئوية التراكمية للتعبير عن تراكم القيم في سلسلة من الأعداد. لحساب النسب المئوية التراكمية، يجب جمع القيم المتتالية ثم تقسيمها على إجمالي القيم.
تطبيقات الأعداد النسبية في الحياة اليومية
في حياتنا اليومية، نجد الأعداد النسبية تلعب دورًا حاسمًا في مجموعة متنوعة من المجالات. هنا بعض الأمثلة على كيفية استخدامها في حياتنا اليومية.
أمثلة لاستخدام الأعداد النسبية في المجالات المختلفة
1. المالية: تستخدم الأعداد النسبية في مجال التمويل والمالية لتقدير أداء الشركات وتوقعاتها المستقبلية. يتم استخدامها أيضًا في تقييم العائد على الاستثمار وحساب نسبة الدين إلى حقوق الملكية.
2. المسح الإحصائي: يتم استخدام الأعداد النسبية في المسح الإحصائي لتحليل وتفسير المجموعات الكبيرة من البيانات. يتم استخدامها في حساب المتوسطات والنسب المئوية وتقدير الانحراف المعياري.
3. التسويق: يتم استخدام الأعداد النسبية في مجال التسويق لتقييم نجاح الحملات التسويقية وقياس معدلات الاستجابة للعملاء. تستخدم أيضًا لحساب مؤشرات الرضا العام ونسبة الانتشار للعلامة التجارية.
4. الطب والصحة: يتم استخدام الأعداد النسبية في تقدير وتحليل عدد تجارب المرضى على الأدوية أو في دراسات سوابق. يستخدم أيضًا لحساب معدلات الإصابة بأمراض معينة وتقدير فاعلية العلاج.
الأعداد النسبية لها تطبيقات عديدة في حياتنا اليومية وفي مختلف المجالات. فهمها واستخدامها بشكل صحيح يمكن أن يساهم في اتخاذ قرارات أفضل وفهم أفضل للبيانات التي نتعامل معها يوميًا.
النسب المئوية والنسب المئوية الموزونة
يُعتبر الاعتماد على النسب المئوية والنسب المئوية الموزونة من الأدوات التحليلية الهامة في مجال الإحصاءات والتحليل. تساهم هذه النسب في تقديم صورة واضحة للمعطيات وتجعل من السهل فهمها وتحليلها.
النسب المئوية تعبر عن العلاقة بين جزء من مجموعة والمجموعة ككل بوحدات قياس مئوية. وتحسب النسب المئوية بقسمة العدد الجزئي على العدد الكلي ثم ضرب الناتج في 100. على سبيل المثال، إذا كان هناك 50 من أصل 200 شخص يحملون شهادة جامعية، فإن النسبة المئوية تكون 25٪.
تُستخدم النسب المئوية الموزونة في بعض الأحيان لتعكس أهمية المتغيرات المختلفة وتأثيرها على النتائج. يتطلب حساب النسب المئوية الموزونة ضرب كل قيمة بعامل الوزن المناسب وجمع هذه القيم ثم قسمتها على مجموع الأوزان. يُستخدم هذا التقدير في مجالات مثل التقييم المالي والاستطلاعات الرأي وتحليل الأداء.
في النهاية، يعد استخدام النسب المئوية والنسب المئوية الموزونة أداة قوية لفهم وتحليل البيانات بشكل كفء. إذا كنت ترغب في اتخاذ قرارات مستنيرة وفعالة، فيُنصح باستخدام هذه الأدوات في تحليلك.
النسب المتساوية وغير المتساوية
عند الحديث عن الأعداد النسبية، فإنه من المهم أن نفهم الفرق بين النسب المتساوية والنسب غير المتساوية. هذا لأن كل منها يمثل طريقة مختلفة للتعبير عن العلاقات بين الأعداد.
الفرق بين النسب المتساوية والنسب غير المتساوية
النسبة المتساوية هي عبارة عن اعتبار قدر متماثل بين كميتين أو أكثر. على سبيل المثال، إذا كان لديك 4 تفاحات و8 تفاحات، فإن النسبة بين عدد التفاحات هي 1:2. وهذا يعني أن عدد التفاحات مضاعف لعدد التفاحات.
أما النسب غير المتساوية، فهي تشير إلى اعتبار قدر غير متماثل بين كميتين أو أكثر. على سبيل المثال، إذا كان لديك 3 تقاويم و6 أقلام، فإن النسبة بين عدد التقويمات والأقلام هي 1:2. وهذا يعني أنه عند زيادة عدد التقاويم بمعدل واحد، ستزداد عدد الأقلام بمعدل اثنين.
فهم الفرق بين النسب المتساوية والنسب غير المتساوية يمكن أن يساعد في فهم كيفية تحليل البيانات والتفاعل بين الأعداد في سياقات مختلفة.
النسب المعكوسة والنسبة المتساوية
في علم الرياضيات، النسب المعكوسة تستخدم لتمثيل العلاقة المقلوبة بين قيمتين. على سبيل المثال، إذا كان لدينا نسبة 3:2 فإن النسبة المعكوسة لها ستكون 2:3. لحساب النسب المعكوسة، يجب تبديل المكان بين العددين في النسبة.
أما بالنسبة للنسبة المتساوية، فهي تستخدم عندما يكون هناك نفس العدد من الأجزاء في العلاقة. مثلا، إذا كانت النسبة هي 1:1 فإن هذه تعبر عن نسبة متساوية. وتستخدم الأشكال المتساوية في الرياضيات وغيرها من التطبيقات، مثل تقاسيم الأراضي أو توزيع الموارد.
في الختام، النسب المعكوسة والنسبة المتساوية هما مفهومان مهمان في الرياضيات يستخدمان لتمثيل العلاقات المقلوبة والعلاقات المتساوية على التوالي. فهم هامان للاستخدام في مجموعة واسعة من التطبيقات في الحياة اليومية والعلمية.
النسبة النسبية والمعادلات النسبية
تعد النسبة النسبية واحدة من المفاهيم الرئيسية في الرياضيات والقدرة على حل المشاكل. تستخدم لتحديد العلاقة المئوية بين عددين أو مجموعتين. يستخدم هذا المفهوم على نطاق واسع في مجالات مثل المالية والإحصاءات والأعمال وغيرها.
تُمثل النسبة النسبية بشكل عام بأرقام كسورية أو بالأعشار. يُمكن استخدام المعادلات النسبية لحل مشكلات تتعلق بالنسبة النسبية. يتضمن ذلك حساب قيمة مجهولة في نسبة قائمة على قيم معروفة.
في التطبيقات العملية ، يتم استخدام المعادلات النسبية لحل مشاكل النسبة النسبية المستخدمة في الصناعة والتجارة والتمويل وغيرها. تساعد هذه الأدوات في حل المعادلات وحساب القيم المجهولة في سياقات مختلفة.
إذا كنت ترغب في حل مشكلات الأعداد النسبية ، فإن استخدام المعادلات النسبية يمكن أن يكون أداة قوية لمساعدتك على فهم وحل التحديات التي تواجهها في هذا المجال.
التناسب العكسي والتناسب المباشر
عند دراسة الأعداد النسبية، يُعتبر التناسب العكسي والتناسب المباشر مفاهيمًا أساسية يجب فهمها. على الرغم من أنهما متشابهان إلى حد ما، إلا أنهما يختلفان في طريقة حسابهما وتمثيلهما.
الفرق بين التناسب العكسي والتناسب المباشر وكيفية حسابهما
التناسب المباشر: في التناسب المباشر، يزداد قيمة العددين معًا بنفس المقدار. على سبيل المثال ، إذا كان هناك 3 أشخاص يحصلون على 100 دولار كلًا منهم، فإن ارتفاع عدد الأشخاص سيزيد من إجمالي المبلغ المالي.
التناسب العكسي: في التناسب العكسي، يُظهر الزيادة في قيمة عامل واحد نقصًا في قيمة العامل الآخر. على سبيل المثال ، إذا كانت سرعة السيارة تتناسب عكسيًا مع الزمن، فكلما زاد الزمن، انخفضت السرعة.
لحساب التناسب المباشر، يجب ضرب قيمة واحدة بالنسبة التي ترغب في تطبيقها. أما في التناسب العكسي، فيجب ضرب قيمتين معًا للحصول على القدر العكسي.
من المهم فهم هذه المفاهيم لتطبيقها في حل المشكلات وفهم العلاقات بين الأعداد. سواء كنت تعمل في مجال التجارة أو العلوم أو أي نشاط ينطوي على الأعداد النسبية، فإن فهم هذه المفاهيم سيساعدك على إجراء حسابات صحيحة واتخاذ قرارات مستنيرة.
استخدام الأعداد النسبية في المجالات العلمية والاقتصادية والإحصائية
تُستخدم الأعداد النسبية في مجموعة واسعة من المجالات، بدءًا من المجالات العلمية وحتى المجالات الاقتصادية والإحصائية. يعتبر استخدام هذه الأعداد طريقة فعالة للتعبير عن النسب والنسب المئوية في العديد من السياقات.
أمثلة لاستخدام الأعداد النسبية في المجالات المتعددة
- في المجال العلمي، تستخدم الأعداد النسبية للوصول إلى مقاييس دقيقة مثل نسبة التغير في التركيز أو نسبة تفاعلات كيميائية.
- في المجال الاقتصادي، يمكن استخدام الأعداد النسبية لقياس أداء الشركات أو تطور سوق معين.
- في المجال الإحصائي، تُستخدم الأعداد النسبية لتحليل البيانات وتوجيه القرارات المستندة إلى المعلومات.
باختصار، الأعداد النسبية تعتبر أداة هامة في التحليل والتقييم في مجموعة متنوعة من المجالات. يمكن استخدامها لفهم وتحليل التغيرات والنسب بطريقة مرئية ويسهل فهمها. سواء كنت طالبًا يدرس العلوم أو محللاً اقتصاديًا أو باحثًا إحصائيًا، ستكون الأعداد النسبية أداة قيمة في عملك.

