قانون محيط الدائرة ومساحتها هو المسافة التي تحيط بالدائرة، أو بمعنى آخر، هو طول الخط المنحني الذي يشكل الحدود الخارجية للدائرة. يعتبر محيط الدائرة من المفاهيم الهامة في الرياضيات، حيث يتم استخدامه في حسابات المساحات والأحجام والمعادلات الهندسية المختلفة.
قانون محيط الدائرة ومساحتها التعبير الرياضي لمحيط الدائرة
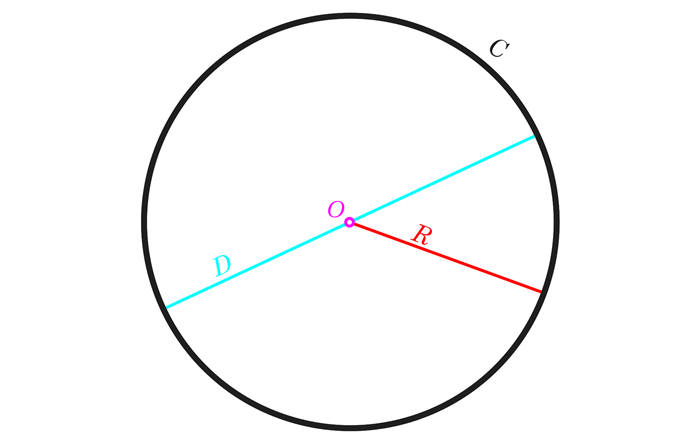
تعبِّر عن محيط الدائرة بواسطة القاعدة العامة الآتية:
محيط الدائرة (P) = 2 × نصف قطر الدائرة (r) × قيمة العدد الثابت القريب إلى قيمة النسبة بين محيط الدائرة وقطرها (π)
أو بصورة أكثر تبسيطًا:
P = 2πr
حيث:
- P يمثل محيط الدائرة.
- r يمثل نصف قطر الدائرة.
- Π يمثل العدد الثابت القريب لقيمة نسبة محيط الدائرة إلى قطرها، وهو يقرب إلى قيمة تقريبية أكثر تعبيرًا عن النسبة بدقة (3.14159).
مع معرفة هذا التعبير الرياضي، يمكن للرياضيين حساب محيط الدائرة بسهولة، مما يساعدهم في حل العديد من المشكلات الرياضية المتعلقة بالدوائر والأشكال ذات الصلة.
للمزيد من المعلومات والتفاصيل حول محيط الدائرة، يمكنك زيارة هذا الرابط:
انتظر 25 ثانية لظهور الرابطhttps://ar.wikipedia.org/wiki/دائرة_(تمهيد)
قانون محيط الدائرة
قانون محيط الدائرة هو قاعدة رياضية تسمح لنا بحساب محيط الدائرة باستخدام نصف قطر الدائرة. يمكن استخدام هذا القانون في العديد من المجالات، مثل الهندسة وعلوم الفضاء وغيرها من التطبيقات. صيغة قانون محيط الدائرة هي كالتالي:
محيط الدائرة = 2 × نصف قطر الدائرة × الثابت (π)
حيث أن “π” يمثل الثابت الذي يتم تقريبه بقيمة تقريبية تعادل 3.14159.
شاهد أيضًا: محيط المثلث ومساحة المثلث بكل القواعد
كيفية حساب محيط الدائرة باستخدام القانون
لحساب محيط الدائرة باستخدام قانون محيط الدائرة، يجب اتباع الخطوات التالية:
- قم بقياس نصف قطر الدائرة باستخدام أداة قياس مناسبة.
- أضف نصف قطر الدائرة إلى قيمة الثابت “π” واحسب الناتج حسب الصيغة السابقة.
- الناتج هو قيمة محيط الدائرة بالوحدة المطابقة لوحدة نصف قطر الدائرة.
مثال:
لنفترض أنه لدينا دائرة بنصف قطر يساوي 5 سم. سنستخدم قانون محيط الدائرة لحساب محيطها بالنحو التالي:
محيط الدائرة = 2 × 5 سم × 3.14159
محيط الدائرة ≈ 31.4159 سم
لذا، محيط هذه الدائرة تقريبًا يساوي 31.4159 سم.
من المهم أن نلاحظ أن قانون محيط الدائرة صيغة بسيطة وسهلة الاستخدام، ويمكن استخدامه لحساب محيط أي دائرة عن طريق معرفة قيمة نصف قطرها.
العلاقة بين قطر الدائرة ومحيطها
العلاقة الرياضية بين قطر الدائرة ومحيطها
في الرياضيات، هناك علاقة هامة بين قطر الدائرة ومحيطها. إذا كانت قيمة قطر الدائرة معروفة، يمكن استخدامها لحساب محيط الدائرة. العلاقة الرياضية بين قطر الدائرة ومحيطها هي كالتالي:
محيط الدائرة = قطر الدائرة × ط
حيث تمثل “ط” قيمة ثابتة تساوي تقريبًا 3.14159 أو تقريبًا 3.14.
شاهد أيضًا: معنى اسم ايهم في اللغة العربية وصفاته بالتفصيل
كيفية استخدام قطر الدائرة لحساب محيطها
لحساب محيط الدائرة باستخدام قطرها، يمكن اتباع الخطوات التالية:
- تحديد قيمة قطر الدائرة.
- ضرب قيمة قطر الدائرة في قيمة ثابتة “ط” (تقريبًا 3.14) للحصول على محيط الدائرة.
مثال:
إذا كان لدينا قطر دائرة بقيمة 10 وحدات، يمكننا حساب محيط الدائرة باستخدام العلاقة التي سبق ذكرها:
محيط الدائرة = 10 × 3.14 = 31.4 وحدة
بالتالي، محيط الدائرة سيكون 31.4 وحدة عندما يكون قطر الدائرة بقيمة 10 وحدات.
يرجى الاطلاع على انتظر 25 ثانية لظهور الرابطهنا لمزيد من المعلومات حول الدوائر ومحيطاتها في الرياضيات.
IV. العلاقة بين القطر والمساحة
العلاقة الرياضية بين قطر الدائرة ومساحتها
في الرياضيات، هناك علاقة رياضية بسيطة بين قطر الدائرة ومساحتها. يتمثل ذلك في القاعدة التالية:
مساحة الدائرة = (نصف قطر الدائرة)^2 × (طول القطر)
هذه العلاقة تساعد في حساب مساحة الدائرة إذا كنت تعرف قطرها.
كيفية استخدام القطر لحساب مساحة الدائرة
إذا كنت تعرف طول القطر، يمكنك استخدام العلاقة المذكورة أعلاه لحساب مساحة الدائرة. إليك الخطوات البسيطة لحساب ذلك:
1. قم بقسم طول القطر على 2 للحصول على نصف قطر الدائرة.
2. قم برفع النصف قطر إلى الأس الثاني (أي ضربه بنفسه) للحصول على مربع النصف القطر.
3. ضرب مربع النصف قطر بطول القطر، وهذا سيعطيك مساحة الدائرة.
مثلاً، إذا كان لديك دائرة قطرها 10 وحدات، فيجب أن تقوم بحساب النصف قطر والنصف قطر المربع وأخيراً ضرب النصف قطر المربع بطول القطر للحصول على مساحة الدائرة.
تذكر أن العلاقة المذكورة أعلاه تعتبر قاعدة عامة في الرياضيات لحساب مساحة الدائرة ويمكن استخدامها في جميع الدوائر بغض النظر عن حجمها.
شاهد أيضًا: معنى اسم ايهم في اللغة العربية وصفاته بالتفصيل
أمثلة وتطبيقات عملية
أمثلة عملية لحساب محيط الدائرة بواسطة القانون
أمثلة عملية لحساب مساحة الدائرة بواسطة القطر
استخدامات محيط الدائرة في الحياة اليومية
استخدامات محيط الدائرة في الهندسة المعمارية
في الهندسة المعمارية ، يعتبر محيط الدائرة من المفاتيح الأساسية لحسابات تصميم المنشآت والمباني. هناك العديد من الطرق التي يمكن استخدام محيط الدائرة فيها ، بما في ذلك:
1. حساب مساحة الأرض: يمكن استخدام محيط الدائرة لحساب مساحة الأرض لتحديد المساحة الكلية للمبنى وتخطيط المشروعات العقارية.
2. تصميم المسابح: يمكن أن يساعد محيط الدائرة في تصميم المسابح وحساب حجم المياه اللازمة لملء المسبح بشكل صحيح.
3. تخطيط الحدائق والمناظر الطبيعية: من خلال استخدام محيط الدائرة ، يمكن تخطيط المسارات المنحنية وتحديد أحجام المساحات الخضراء في الحدائق والمناظر الطبيعية.
4. تصميم الدواجن والحظائر الحيوانية: في صناعة الدواجن وتربية الحيوانات ، يمكن استخدام محيط الدائرة في تصميم الأقفاص وحساب مساحة الدواجن المطلوبة لحيواناتك.
استخدامات محيط الدائرة في الصناعات المختلفة
بالإضافة إلى الهندسة المعمارية ، يتم استخدام محيط الدائرة في العديد من الصناعات المختلفة بما في ذلك:
1. الصناعة البحرية: في تصميم السفن والقوارب ، يعتبر محيط الدائرة جزءًا هامًا من عملية حساب الاستقرار والتوزان للسفينة.
2. الصناعة العامة والتصنيع: يمكن استخدام محيط الدائرة في تصنيع الأسلاك والأنابيب والأجزاء الدقيقة الأخرى التي تحتاج إلى تصميم دقيق.
3. تطبيقات الروبوت: في التصميم والبرمجة للروبوتات ، يمكن استخدام محيط الدائرة لتحديد نصف القطر الأمثل للحركة الدورانية للروبوت.
هذه المثالات فقط لبعض الاستخدامات الشائعة لمحيط الدائرة في الحياة اليومية والصناعات المختلفة. تظهر أهمية فهم واستخدام هذا النوع من القياسات في العديد من مجالات حياتنا وعملنا.
شاهد أيضًا: ما هو الرصد ؟ وطريقة التعامل معه عند المواجهة
العلاقة بين قوانين محيط الدائرة ومساحتها

العلاقة بين القوانين الرياضية لمحيط الدائرة ومساحتها
في الرياضيات، هناك علاقة وثيقة بين قوانين محيط الدائرة ومساحتها. يمكن استنتاج قوانين محيط الدائرة من قوانين مساحتها والعكس بالصورة التالية:
- القاعدة العامة: إذا كان لدينا معلومات عن محيط الدائرة، فيمكننا استخدام القاعدة العامة لحساب مساحتها. وعلى العكس، إذا كان لدينا معلومات عن مساحة الدائرة، يمكننا استخدام القاعدة العامة لحساب محيطها.
- قوانين محيط الدائرة: هناك عدة قوانين في الرياضيات تساعد في حساب محيط الدائرة، مثل قانون محيط الدائرة بالنسبة لقطرها وقانون محيط الدائرة بالنسبة لنصف قطرها. يمكن استخدام هذه القوانين لحساب محيط الدائرة إذا كان لدينا المعلومات المناسبة.
- قوانين مساحة الدائرة: هناك أيضًا قوانين في الرياضيات تساعد في حساب مساحة الدائرة، مثل قانون مساحة الدائرة بالنسبة لقطرها وقانون مساحة الدائرة بالنسبة لنصف قطرها. يمكن استخدام هذه القوانين لحساب مساحة الدائرة إذا كانت لدينا المعلومات المناسبة.
شاهد أيضًا: معنى اسم ايهم في اللغة العربية وصفاته بالتفصيل
كيفية استخدام قانون محيط الدائرة لحساب مساحتها والعكس
يمكن استخدام قوانين محيط الدائرة لحساب مساحتها والعكس على النحو التالي:
- إذا كان لدينا معلومات عن محيط الدائرة، فيمكننا استخدام القاعدة العامة لحساب مساحتها. قد يتطلب ذلك استخدام قانون محيط الدائرة بالنسبة لقطرها أو قانون محيط الدائرة بالنسبة لنصف قطرها، اعتمادًا على المعلومات المتاحة.
- إذا كان لدينا معلومات عن مساحة الدائرة، فيمكننا استخدام القاعدة العامة لحساب محيطها. قد يتطلب ذلك استخدام قانون مساحة الدائرة بالنسبة لقطرها أو قانون مساحة الدائرة بالنسبة لنصف قطرها، اعتمادًا على المعلومات المتاحة.
- يمكن استخدام القوانين المذكورة لمعرفة العلاقة بين محيط الدائرة ومساحتها وتوجيه الحسابات بناءً على المعلومات المتاحة.
يمكن الاطلاع على المزيد من المعلومات حول قانون محيط الدائرة ومساحتها في انتظر 25 ثانية لظهور الرابطهذا الرابط.
قوانين محيط الدوائر الكبيرة
تعتبر الدوائر الكبيرة من الأشكال الهندسية المهمة في الرياضيات، ومعرفة كيفية حساب محيطها يعتبر أمراً ضرورياً لحل العديد من المسائل والتطبيقات. هنا سوف نقدم قوانين محيط الدوائر الكبيرة وكيفية حسابها.
قوانين محيط الدوائر الكبيرة وتطبيقاتها
هناك قواعد هامة لحساب محيط الدوائر الكبيرة وتطبيقاتها في الحياة العملية والرياضيات. إليك بعض القوانين الهامة:
• قانون محيط الدائرة: محيط الدائرة يتناسب مع قطرها بواقع علاقة رياضية ثابتة تساوي 𝟯.١٤١٥.
• حساب محيط الدوائر باستخدام القطر: يُعتبر القطر من العناصر الرئيسية لحساب محيط الدائرة. يمكن استخدامه في العلاقة 𝟯.١٤١٥ × القطر لحساب محيط الدائرة.
• حساب محيط الدوائر باستخدام القطر: يمكن استخدام النصف القطر (r) بدلاً من القطر في العلاقة 𝟯.١٤١٥ × 𝟮 × النصف القطر لحساب محيط الدائرة.
هذه القوانين تستخدم في العديد من المجالات مثل البناء والهندسة المعمارية والعلوم الطبية وغيرها.
لمعرفة المزيد عن الدوائر الكبيرة وقوانينها في الرياضيات، يمكنكم زيارة الرابط التالي: انتظر 25 ثانية لظهور الرابطدائرة (ويكيبيديا).
كيفية حساب محيط الدوائر الكبيرة باستخدام القوانين الرياضية
لحساب محيط الدوائر الكبيرة، يمكن اتباع الخطوات التالية:
1. قياس القطر أو النصف القطر: قم بقياس القطر أو النصف القطر للدائرة باستخدام أدوات القياس المناسبة.
2. احسب محيط الدائرة باستخدام القطر أو النصف القطر: مع وجود القطر أو النصف القطر، يمكنك استخدام القوانين الرياضية المشار إليها سابقًا لحساب محيط الدائرة.
3. أدخل القيم واحسب محيط الدائرة: بمجرد الحصول على القيم المطلوبة، أدخلها في العلاقة المناسبة واحسب محيط الدائرة.
قد تحتاج أيضًا إلى معرفة كيفية حساب مساحة الدوائر الكبيرة. لمزيد من المعلومات حول هذا الموضوع، يمكنكم زيارة الرابط التالي: انتظر 25 ثانية لظهور الرابطدائرة (ويكيبيديا).
هذه هي القوانين الرئيسية لحساب محيط الدوائر الكبيرة وتطبيقاتها. يمكن استخدام هذه القوانين في العديد من مجالات العلوم والهندسة وغيرها.
مميزات وفوائد قانون محيط الدائرة
مميزات استخدام قانون محيط الدائرة في الحسابات
- يسهل قانون محيط الدائرة حساب محيط الدوائر بسرعة ودقة.
- يعتبر قانون محيط الدائرة من أساسيات الرياضيات المتعلقة بالهندسة الهندسة والهندسة الميكانيكية.
- يمكن استخدام قانون محيط الدائرة في حسابات الطوافة والمساحة لأشكال هندسية أخرى مثل البيضاوي والمستطيل.
فوائد استخدام قانون محيط الدائرة في الحياة العملية
- يمكن استخدام قانون محيط الدائرة في مجالات مختلفة مثل الهندسة المدنية والهندسة المعمارية وعلوم الحاسوب.
- يوفر قانون محيط الدائرة حلا سريعا وفعالا لحساب محيط دوائر الأنابيب والأسلاك والحلقات وغيرها من الأشكال المدورة.
- يساعد قانون محيط الدائرة في توفير وقت وجهد في الحسابات اليومية المتعلقة بالأشكال الدائرية.
باستخدام قانون محيط الدائرة في الحسابات الخاصة بك، يمكنك تحقيق نتائج دقيقة بسرعة وكفاءة. قانون محيط الدائرة يوفر أيضا فوائد عملية في مجموعة متنوعة من المجالات، ويعتبر أحد الأسس الأساسية للاهتمامات الهندسية والعلمية. لمزيد من المعلومات عن قانون محيط الدائرة، يمكن الاطلاع على انتظر 25 ثانية لظهور الرابطهذا الرابط.
شاهد أيضًا: كمال الأجسام للمبتدئين لتكوين العضلات
ملخص واستنتاجات
ملخص لمحتوى المقالة وأهم النقاط المطروحة
في هذه المقالة تم استعراض مفهوم قانون محيط الدائرة ومساحتها في الرياضيات. تم توضيح أن محيط الدائرة يعتمد على القيمة المعروفة باسم طول قطر الدائرة (أو الهمسة) المضروبة في القيمة المعروفة باسم طول القطر. وأن مساحة الدائرة يتم حسابها عن طريق ضرب القيمة المعروفة باسم نصف قطر الدائرة في نفسها ومراكزها. تم استعراض الصيغ التي تستخدم لحساب كل من المحيط والمساحة، مع توضيح الوحدات المستخدمة عادة في القياسات.
استنتاجات ونصائح في استخدام قانون محيط الدائرة
- قانون محيط الدائرة يعد أحد القوانين الأساسية في الرياضيات ويستخدم في العديد من المجالات مثل الهندسة والعمارة وعلوم الحاسوب.
- من المهم فهم كيفية حساب محيط ومساحة الدائرة بشكل صحيح لتطبيقها في المشاكل العملية.
- يمكن استخدام القوانين المشتقة من قانون محيط الدائرة لحساب محيطات ومساحات الأشكال الهندسية الأخرى مثل الدوائر المجاورة والأقواس.
- للمزيد من المعلومات حول قانون محيط الدائرة وتطبيقاته، يمكن الاطلاع على مقالة انتظر 25 ثانية لظهور الرابطدائرة على ويكيبيديا.
باستخدام هذه المعلومات والتوجيهات، يمكن للأفراد استخدام قانون محيط الدائرة بشكل صحيح وفعال في حساباتهم وتطبيقاتهم العملية.

